Pythagorova věta
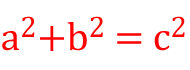Jedná se o jednu z nejznámějších matematických pouček: a2 + b2 = c 2, rovnice známá jako Pythagorova věta. Ve slovním vyjádření zní Pythagorova věta takto:
obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníka se rovná součtu obsahu čtverců nad odvěsnami. Nejmenší celá čísla, která vyhovují uvedené rovnici, jsou 3, 4 a 5: 32 + 42 = 52
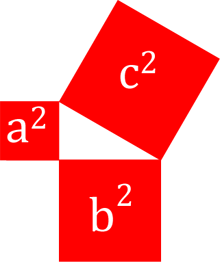
Další známý příklad jsou čísla 5, 12 a 13. V grafické podobě Pythagorovu větu znázorňuje následující obrázek.
Pro důkaz Pythagorovy věty budeme potřebovat čtyři identické pravoúhlé trojúhelníky. Ty poskládám vedle sebe tak, že vytvoří větší čtverec, jak ukazuje obrázek níže.
Obsah každého ze čtyř malých trojúhelníků je roven a * b / 2. Obsah červeného čtverce uprostřed je c2, zatímco obsah celé plochy (velkého čtverce) se rovná
(a + b)2.
Nyní můžeme dát do rovnosti obsah jednotlivých ploch s celkovým obsahem:
(4 * a * b) / 2 + c2 = (a + b)2
Po roznásobení obdržíme:
2 * a * b + c2 = a2 + 2 * a * b + b2
A odtud plyne:
c2 = a2 + b2
Na začátku jsme vycházeli z obecného pravoúhlého trojúhelníku se stranami a, b, c. Tímto jsme dokázali všeobecnou platnost Pythagorovy věty pro libovolný pravoúhlý trojúhelník.
Komentáře k článku