Úrokové riziko dluhopisu

Z analýzy výpočtu vnitřní hodnoty dluhopisu plyne, že tato „správná cena“ dluhopisu je v inverzním vztahu k tržní úrokové míře. Jinými slovy, pokud tržní úroková míra roste, cena dluhopisu klesá a naopak. Úrokové riziko tedy představuje citlivost ceny dluhopisu na pohyb tržních úrokových měr. Toto riziko lze měřit pomocí durace a konvexity.

Durace měří sklon křivky závislosti ceny dluhopisu na úrokové míře a vychází z první derivace ceny dluhopisu podle úrokové míry. Nejznámější druh durace zkonstruoval v roce 1938 Frederick Macaulay. Macaulayova durace (MD) měří průměrnou dobu trvání potřebnou k tomu, aby investor obdržel všechny budoucí příjmy z dluhopisu, a lze ji vypočítat takto:

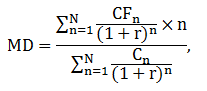
kde CFn jsou roční cash flow vyplácené z dluhopisu: kupony a jmenovitá hodnota vyplacená na konci životnosti, N je počet let do doby splatnosti dluhopisu a r tržní úroková míra

Čím vyšší je hodnota durace, tím více reaguje cena dluhopisu na pohyb úrokových měr a úrokové riziko se tak zvyšuje. S růstem doby splatnosti durace roste, avšak klesajícím tempem. Dluhopisy s vyššími kuponovými platbami mají nižší hodnotu durace v porovnání se stejnými dluhopisy, které mají nízké kupony.

Konvexita měří zakřivení křivky, která vyjadřuje vztah mezi cenou dluhopisu a úrokovou měrou a vychází z druhé derivace ceny dluhopisu podle úrokové míry. Konvexitu (Conv) lze vyjádřit vztahem:

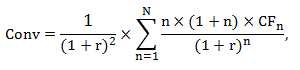
kde uvedené symboly odpovídají výše uvedenému vymezení.

Macaulayovu duraci lze spolu s konvexitou využít k přibližnému stanovení změny ceny dluhopisu v reakci na malou změnu úrokové míry, přičemž právě přidání konvexity tento výpočet zpřesňuje:

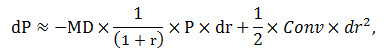
kde dP odpovídá změně ceny dluhopisu, dr je změna úrokové míry a P je výchozí cena dluhopisu.

Komentáře k článku