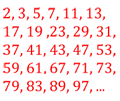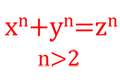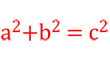Obecná matematika
Kromě finanční matematiky se tyto stránky věnují také ryze matematickým tématům, které naleznete právě v této sekci. Jsou zde články z teorie čísel nebo kryptografie. Najdete tu rovněž algoritmy, matematické důkazy a v neposlední řadě také známé matematické věty.
|
|