Spojité úročení aneb jak počítat s nekonečnem
Spojité úročení je extrémním případem úročení složeného.
Tomu jsme se věnovali minule a řekli jsme si, že se zkracováním úrokového
období efekt složeného úročení roste. Za jinak stejných podmínek (ekonomy
oblíbený předpoklad známý také pod latinským výrazem ceteris paribus)
přinese denní složené úročení vyšší zhodnocení než měsíční, měsíční vyšší než
čtvrtletní, čtvrtletní než roční atd.
Co by se ale stalo, kdybychom se rozhodli úročit neustále? Když zkrátíme úrokové období na nekonečně krátkou dobu, dostaneme spojité úročení. Při měsíčním úročení se připíše úrok 12krát ročně, při denním 365x ročně a při nepřetržitém úročení nekonečněkrát ročně. Nabízí se otázka. Přinese nám spojité úročení v konečném čase nekonečně vysoké zhodnocení? Odpovíme si hned, nepřinese. Spojité úročení má praktický význam, používají ho bankéři a finančníci, zatímco s nekonečnem se potýkají jen matematici, fyzici či filozofové. Jak je možné, že výsledkem nekonečného počtu matematických operací je konečné číslo? Matematik by nám řekl, že to je nejen možné, ale i docela běžné. Jako ekonom můžu potvrdit, že i v našem oboru se to občas stává (krom spojitého úročení se jedná třeba o emisi bezhotovostních peněz).
Nyní už je na čase začít tuhle záhadu řešit a to tak, že si odvodíme vzorec spojitého úročení. Nejprve si zopakujme, jak vypadá obecně složené úročení:
,
kde P0 je počáteční částka, i je úroková sazba vztažená k úrokovému období, n je počet období a Pn částka na konci n-tého období.
Ze stejného vzorce vychází i spojité úročení. Když si uvědomíme, že nekonečně krátkému úrokovému období dopovídá také nekonečně malá úroková sazba, máme skoro vyhráno. Zavedeme si novou proměnnou t, která se bude limitně blížit nekonečnu. Úroková sazba dostane tvar i/t a počet úrokových obdobích je nyní t × n, protože v každém z n období je dalších t období. Pro spojité úročení tak platí:
Tuto limitu jsme schopni spočítat díky objevu jedné matematické konstanty, která byla pojmenována po jednom švýcarském matematikovi. Tou konstantou je Eulerovo číslo, značí se malým e, má přibližnou hodnotu 2,71828... a nekonečně dalších číslic za desetinnou čárkou (je iracionální, podobně jako π nebo √2). Důležité ovšem je, že Eulerovo číslo lze mimo jiné vyjádřit následující limitou:
Když srovnáme obě výše uvedené limity, zjistíme, že se až tolik neliší. Náš vzorec pro spojité úročení potřebujeme upravit tak, aby z čitatele zlomku zmizela úroková sazba a zůstala zde pouze jednička. Po této úpravě se nám navíc musí shodovat proměnné ve jmenovateli zlomku a exponentu (čísle, na které umocňujeme). Obojí provedeme rozšířením zlomků:
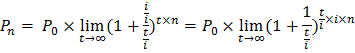
Nyní už stačí substitucí nahradit t/i novou proměnnou (m):
Z poměrně komplikovaného výrazu na začátku jsme několika kroky získali elegantní vztah, který je hledaným vzorcem spojitého úročení. Nekonečno kamsi zmizelo. Všechny proměnné jsou nejen konečná čísla, nýbrž také platí, že pro relativně nízké úrokové sazby (v řádu několika málo procent) se spojité úročení od složeného příliš neliší. Ukážeme si to na stejných příkladech použitých u složeného úročení (více o vlastnostech přirozeného logaritmu, jehož základem je Eulerovo číslo, zde).
Uložených 1000 korun na úrok 10 % p. a. přinese při ročním úročení na konci roku částku 1 100 Kč (platí pro jednoduché i složené úročení). Použitím spojitého úročení získáme zhruba o 5 korun více: 1 000 × e^(0,1×1) = 1 105,17.. Čtvrtletní složené úročení nicméně přinese už téměř 1 104 Kč: 1 000 ×(1+0,1/4)^4 = 1 103,81.. Pouhá čtyři úročení se v tomto případě vyrovnají třem čtvrtinám efektu (3,81 / 5,17), který přinese spojité úročení s nekonečně úrokovými obdobími. Všechny tři typy úročení vypadají v grafickém vyjádření takto.
Srovnání typů úročení (2 roky, úroková sazba 40 % p. a.)
Jedná se o totožný graf, jaký ilustroval sílu složeného úročení. Přidaná modrá křivka potvrzuje, že spojité úročení je ještě silnější. Efekt spojitého úročení ovšem vynikne jen s dostatečně vysokou úrokovou sazbou (40 % ročně je dost). Se zkracujícím se úrokovým obdobím příslušná úroková sazba klesá a křivka složeného úročení se rychle přibližuje ke křivce spojitého úročení. Jak bylo řečeno v samém úvodu, spojité úročení je jen speciálním případem úročení složeného.
Komentáře k článku